RUMUS- RUMUS TURUNAN FUNGSI ALJABAR MATEMATIKA

Fungsi mengungkapkan hubungan antar variabel. Nilai dari variabel-variabel ini dapat nomor atau benda nonnumerical seperti angka geometris, fungsi, atau bahkan benda-benda nonmathematical. Ada berbagai macam fungsi, tapi kami akan berurusan terutama dengan fungsi objek numerik dalam hal x.

Fungsi menjelaskan aturan atau proses yang mengaitkan setiap masukan dari fungsi untuk output yang unik. Ketika kami pertama kali diperkenalkan ke persamaan dua variabel, kita melihat mereka dalam hal x dan y

di mana x adalah variabel bebas dan y adalah variabel dependen. Ketika kita memiliki fungsi, x adalah input dan f (x) adalah output.

dimana f adalah fungsi dari x yang ganda setiap nilai x ditugaskan untuk itu, yaitu

Umumnya fungsi dilambangkan dengan huruf f tapi ini bukan notasi ketat karena surat-surat lain juga dapat digunakan. Biasanya f (x) berlangsung dari nilai y secara eksplisit mengidentifikasi variabel yang independen yang digunakan dalam fungsi.

Alasan mendasar mengapa kita menggunakan notasi ini karena fungsi tidak hanya berurusan dengan persamaan, tetapi sebagai deskripsi verbal dan pemetaan satu elemen yang lain (alam nomor sesuai dengan nomor perdana, misalnya). Fungsi juga ditentukan oleh ekspresi minimal satu variabel. Setelah kami merumuskan aturan untuk ekspresi dalam hal variabel, maka itu adalah fungsi, di mana ekspresi adalah mendefinisikan formula untuk fungsi.

x dikenal sebagai argumen fungsi. Untuk setiap nilai argumen x harus ada hanya satu nilai dari f (x) untuk itu harus dianggap fungsi. Domain fungsi didefinisikan sebagai himpunan yang berisi nilai-nilai yang berbeda dari argumen. Kisaran fungsi didefinisikan sebagai himpunan yang berisi nilai-nilai fungsi untuk domain yang diberikan.

Sebagai contoh, mengingat persamaan

y adalah fungsi dan x adalah argumen.

Persamaan di atas juga dapat ditulis sebagai

dari mana kita dapat melihat secara eksplisit y yang merupakan fungsi dari x.
Untuk di atas, mengingat domain dari x sebagai {0,1,2}, berbagai fungsi dapat dihitung dengan menggantikan nilai-nilai yang berbeda dari x ke dalam persamaan untuk menghasilkan hasil set:

Vertikal Jalur Tes

Fungsi mendefinisikan hubungan untuk sebuah ekspresi untuk memiliki satu output unik untuk setiap masukan. Misalnya, nilai x harus sesuai dengan hanya satu nilai y, tapi lebih dari satu nilai x dapat sesuai dengan nilai y yang sama. Sebuah cara untuk menguji hubungan ini untuk melihat apakah gambar pada grafik adalah fungsi adalah dengan menggunakan uji garis vertikal. Jika kita mampu menarik garis vertikal pada setiap titik pada grafik dan hanya memiliki satu titik persimpangan, maka grafik adalah fungsi. Jika ada lebih dari satu titik persimpangan, itu bukan fungsi.

Mari kita menentukan apakah grafik berikut fungsi.

(1)

Setiap nilai x memiliki nilai unik y. Ini adalah fungsi.
(2)

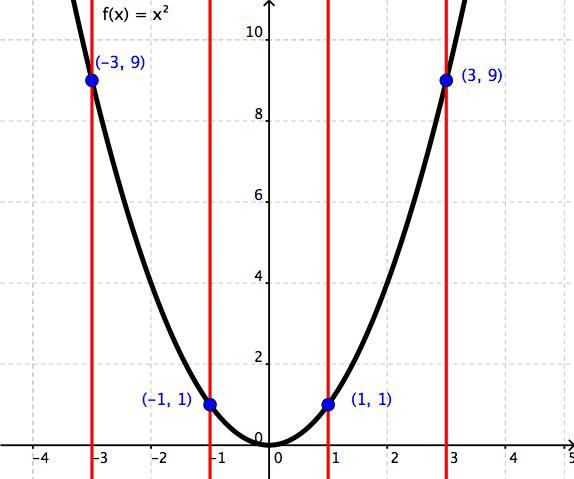
Meskipun dua x nilai mungkin memiliki nilai y yang sama, setiap nilai x hanya memiliki satu nilai y. Ini memang fungsi.
(3)

Kita bisa melihat bahwa setidaknya satu garis vertikal memiliki berpotongan di lebih dari satu titik dengan grafik. Ini bukan fungsi.
(4)

Satu ini, bagaimanapun, adalah fungsi. Dapatkah Anda melihat kesamaan antara grafik ini dan yang terakhir?

Sebuah cara untuk menggunakan tes garis vertikal adalah untuk mengambil penggaris, membuatnya vertikal, dan memindahkannya di sepanjang grafik untuk melihat apakah ada adalah setiap titik di mana ada dua nilai y yang sesuai dengan nilai x.

Fungsi Ganjil dan Bahkan Fungsi

Fungsi dapat ganjil atau genap. Fungsi dikatakan aneh jika mereka memenuhi identitas di bawah ini

yang berarti bahwa setiap kali fungsi membutuhkan argumen negatif (- x), hasilnya selalu sama dengan nilai negatif dari fungsi dengan argumen positif (x).
Sebagai contoh, mengingat fungsi f (x) = 3 (x), pemecahan untuk x = -1

dan karena

fungsi aneh.
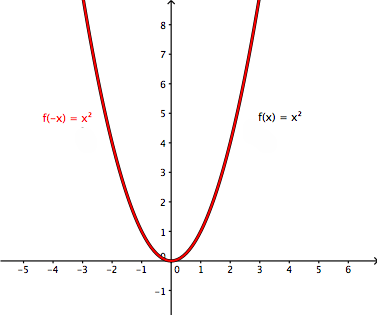
Contoh fungsi yang aneh:
(1)

(2)

Fungsi dikatakan bahkan jika mereka memenuhi identitas di bawah ini

yang berarti bahwa untuk setiap nilai negatif dari argumen (- x), hasilnya selalu sama dengan nilai fungsi dengan argumen positif (x). Dengan kata lain, negatif tidak berpengaruh pada nilai fungsi.
Sebagai contoh, mengingat fungsi

dan juga

Berikut adalah grafik f (x) = x ²

Mengetahui apakah suatu fungsi genap atau ganjil dapat membuatnya jauh lebih mudah untuk memecahkan.

Fungsi Komposit

Fungsi tidak hanya mengambil variabel sebagai argumen tetapi juga dapat mengambil fungsi lain sebagai argumen. Sebagai contoh, mengingat fungsi berikut f (x) dan g (x) di mana

Misalkan Anda diminta untuk memecahkan f (g (x)). Ini akan menjadi yang meminta Anda untuk menemukan f fungsi dari fungsi g (x). Dengan kata lain, gunakan fungsi g (x) sebagai argumen dari fungsi f

tapi ingat bahwa

Komposisi juga dilambangkan sebagai

Inverse Fungsi

Beberapa fungsi memiliki invers yang memiliki efek kehancuran operasi apa pun fungsi yang dilakukan pada variabel. Kebalikan dari fungsi dapat dianggap sebagai kebalikan dari fungsi tersebut. Misalnya, mengingat fungsi